Find The Resultant Electric Field At Point P
A 68 103 NC B 80 103 NC C 39 103 NC D 27 103 NC E 17 104 NC Ans. E x x10 E y x10 NC or E x10 NC at angle degrees.

Electric Field Due To The System Of Point Charges
GOAL Use the superposition principle to calculate the electric field due to.

Find the resultant electric field at point p. Resultant electric field at point P. What is the electric field intensity E at point P. Enet Ex2 Ey2.
The field at point P due to the pinholes would be K 1 Vr 1 t t 1 and K 2 Vr 2 t t 2 respectively where r 1 and r 2 define the positions of P 1 and P 2 t 1 and t 2 are the times taken by the light to travel to P from P 1 and P 2 and K 1 and K 2 are imaginary constants that depend on the geometry and size of the respective pinhole and its distance from the point P. Suppose we have to calculate the electric field intensity or strength at any point P due to a point charge Q at O. E 2 45 x 10 3 1 x 10-2.
A A is negative and B is positive. Find the electric field at point P in Fig. Eynet Ey Ey1 Ey2.
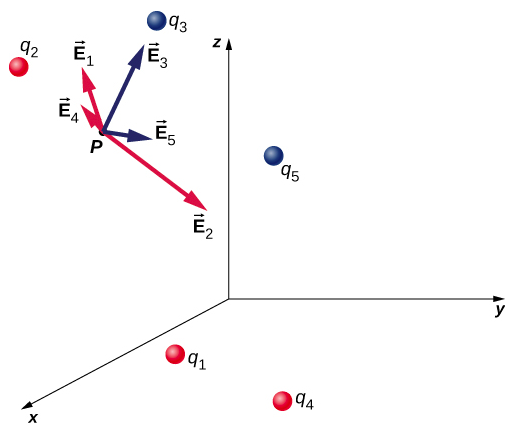
The integral of such dEs will then give the desired field. The electric field 2. The resultant electric field at point P is the vector sum of the fields.
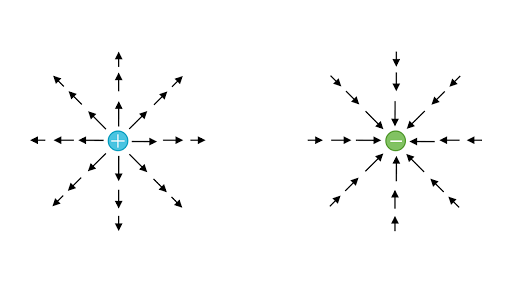
The direction of the electric field is the direction of the force the positive test charge would experience. If the electric field is due to more than one charge Fig. First we note that the direction of E is toward Q down.
To find the electric field of a charge distribution at point P in space it must be divided into infinitesimal charges dq that can act as point charges and dE the field of each dq be calculated at that point. Electric Field Due to a Point Charge Example. The total electric field at point A.
4000 N 2 x 10 C. D If a new charge q3 240 nC was brought to point P. Same for any charge placed at.
1nC 1x 10C 1 42 6m 6m 600 6m 91 a Find the electric field at point P due to charge 1 E. Charge B is positive so that the direction of the electric field points away from Q B to the left. E 1 360 x 10 3 16 x 10-2 E 1 225 x 10 5 NC.
This is called superposition of electric fields. Two thin parallel conducting plates. To find the direction of the electric field vector due to a point charge at any point of space we perform a thought experiment that consist in placing a positive test charge at this point.
The electric field 1. The components along the dipole axis add up. Which statement identifies the charges of and B.
Three identical point charges each of 10 nC are placed along a vertical line as shown in the FIGURE 3. The field E would be the same. E 2 x 10.
The electric field for q is directed radially outwards from the charge while for - q it will be radially directed inwards. E 2 9 x 10 95 x 10-6 1 x 10-1 2. Charge A is negative so that the direction of the electric field points toward Q A to the left.
The resultant voltage is simply the sum of the individual voltages. Exnet Ex Ex1 Ex2. The magnitude and direction of electric field at point P.
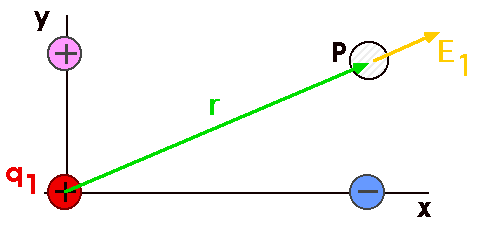
A positive test charge located at point P would experience a repulsive force as q 1 is positive and therefore E 1 goes outwards q 1. E 1 k q 1 r 1 2. The magnitude of the electric field at point P.
Then resultant Electric field at point P is given by To find the resultant electric field intensity due to the dipole at point P we will represent EA and EB by the two adjacent sides PL and PM of a parallelogram. E 1 9 x 10 940 x 10-6 4 x 10-1 2. The resultant field equals the vector sum of the fields due to each individual charge Fig.
The net electric field at point P is the vector sum of electric fields E1 and E2 where. C Find the resultant electric field at point P. B Find the electric field at point P due to charge 2.
5 7 910 110. In the following system. The electric field at an arbitrary point due to a collection of point charges is simply equal to the vector sum of the electric fields created by the individual point charges.
Electric field at point P due to charge at distance R E 1 4 o R 2 q towards left Electric field at point P due to charge at distance 2 R E 2 4 o 2 R 2 q 1 6 o R 2 q towards right. The formula E kqr 2 in its vector form applies to point charges. The resultant of the electric field at point P.
Recall that positive charges are sources of electric field. Say you want to calculate the electric field E3 at a point at x3 and y5 you would then use the equation in the following manner. E 2 45 x 10 5 NC.
V V 1. What is the electric field at the point P. 8 K O .
Then diagonal PN represents the resultant Electric field due to the dipole acting along Px. EXAMPLE 155Electric Field Due to Two Point Charges The resultant electric field at P equals the vector sum 1 2 where 1 is the field due to the positive charge q1 and 2 is the field due to the negative charge q2. B and B are both negative.
Find the net force on charge 3 4. E q E. Page 3 Which diagram best illustrates the electric field between charges A and B.
E E A E B. Consider a collection of point charges q 1 q 2q 3. E3 frac14pi epsilon_0 fracq3hatx 5haty Sorry P is located at 0 in the x direction.
E 45 x 10 5 9 x 10 5. B C D B C D The diagram below represents the electric field lines in the vicinity of two isolated electrical charges A and B. So in order to find the net electric field at point P we will have to analyze the electric field produced by each charge and how they interact cancel or add together.
2b above find the electric field at P due to each charge. 91 200 nC and q2 -150 nC. Thus the resultant field at point P would be.
Therefore the resultant electric field at point P is given as E - E_ q E_ -q cos The negative sign shows that the field is opposite to the dipole moment of the dipole E -2qa 4_0 x2a2 32. E 2 k q 2 r 2 2. To find the electric field at some point P due to this collection of point charges superposition principle is used.
What is the electric field at the point P. The resultant electric field can also be found using the triangle law of addition. F E q 2 nC.
Resultant of the electric field. 3 q 1 -10 x 10 -6 C and q 2 30 x 10 -6 C. Then find the net field by integrating over the length of the rod The charge per unit length on the thin semicircular wire shown below is.
Solve this problem by first considering the electric field at P due to a small segment dx of the rod which contains charge. Find the magnitude of the resultant electric field at a point P 60 cm in front of middle charge.

What Is The Magnitude Of The Dipole S Electric Field At Point P Youtube

Net Electric Field Due To Point Charges Youtube

Important Questions For Class 12 Physics Chapter 1 Electric Charges And Fields Class 12 Important Questions Physics And Mathematics Physics Chemistry Education

In The Figure What Is The Net Electric Potential At Point P Youtube

Determine The Point Other Than Infinity At Which The Total Electric Field Is Zero Youtube

Find The Electric Field At A Point P On The Perpendicular Bisector Of Unifoumly Charged Rod T Youtube

Why Is The Electric Field Zero At This Point Physics Stack Exchange

Eee340lecture 081 Example 3 1 Determine The Electric Field Intensity At P 0 2 0 2 3 Due To A Point Charge Of 5 Nc At Q 0 2 0 1 2 5 Solution Ppt Download
Electric Field Article Electrostatics Khan Academy

Electric Field Lines Multiple Charges Physics
B3 The Electric Field Due To One Or More Point Charges Physics Libretexts

Electric Field Due To Point Charges Physics Problems Youtube

Conductors And Electric Fields In Static Equilibrium Physics
5 5 Electric Field Physics Libretexts

Physics 121 Electricity Magnetism Lecture 3 Electric Field Ppt Download
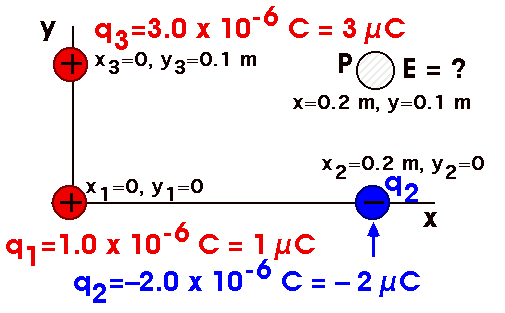

Posting Komentar untuk "Find The Resultant Electric Field At Point P"